Landauer’s Principle is the claim that any computational process that “merges two computational paths” comes with an entropy cost of (at least) k ln 2. This sort of merging is also termed “erasure of information” in the literature. Thus, Landauer’s Principle asserts that there is a minimal cost paid in the creation of thermodynamic entropy whenever we have “erasure of information.” It turns out that this really isn’t true in the way Landauer conceived it, although it does have a counterpart at the quantum level. In a new paper, A. Schlatter and I show that specific physics does not support the equivalence of logical/computational probabilities (based only on ignorance) with thermodynamic probabilities, i.e., those corresponding to Boltzmann’s formula S = k ln Omega. Thus, “erasure of information” does not necessarily create entropy. However, erasure of genuine quantum uncertainty does do so. Here are the details: http://philsci-archive.pitt.edu/22511/
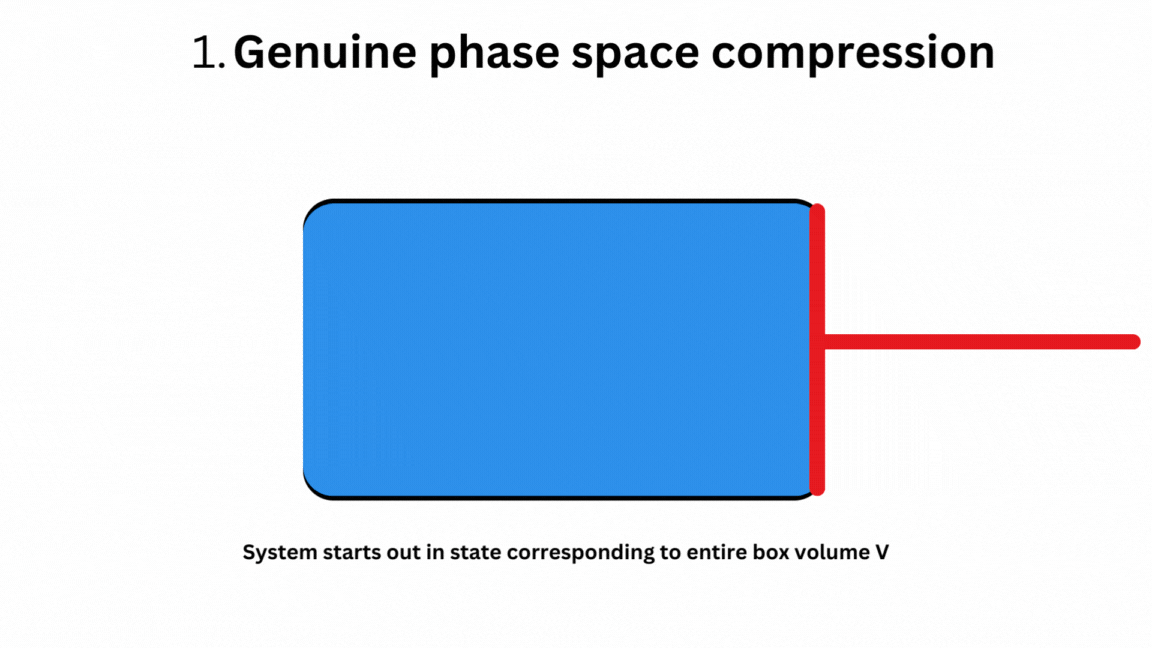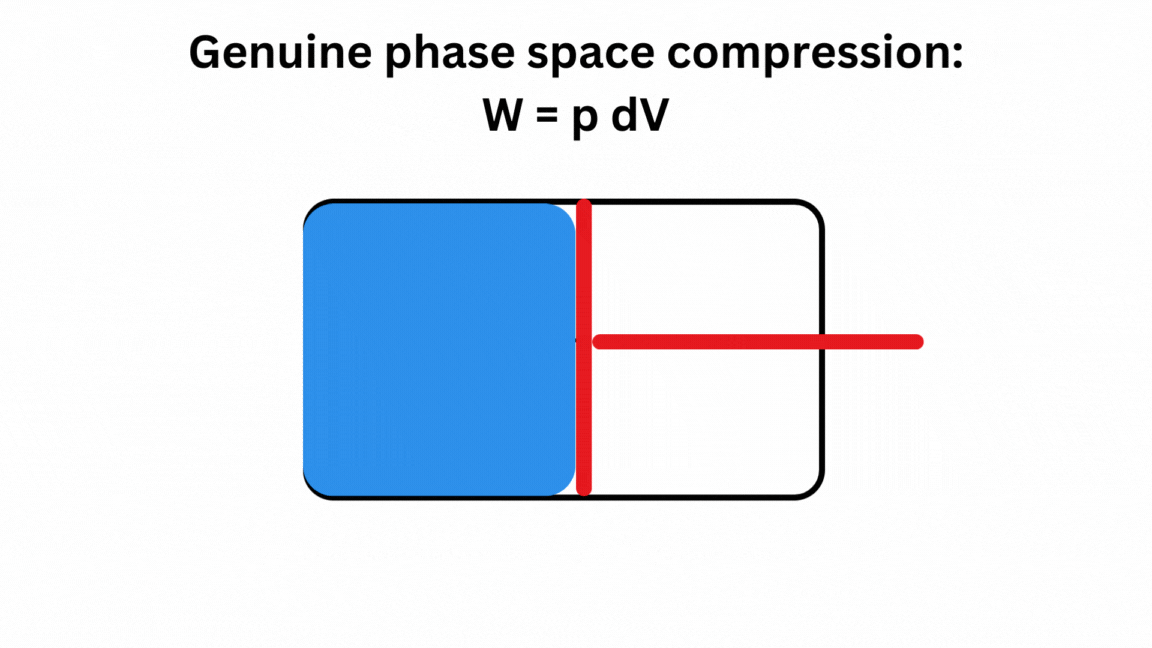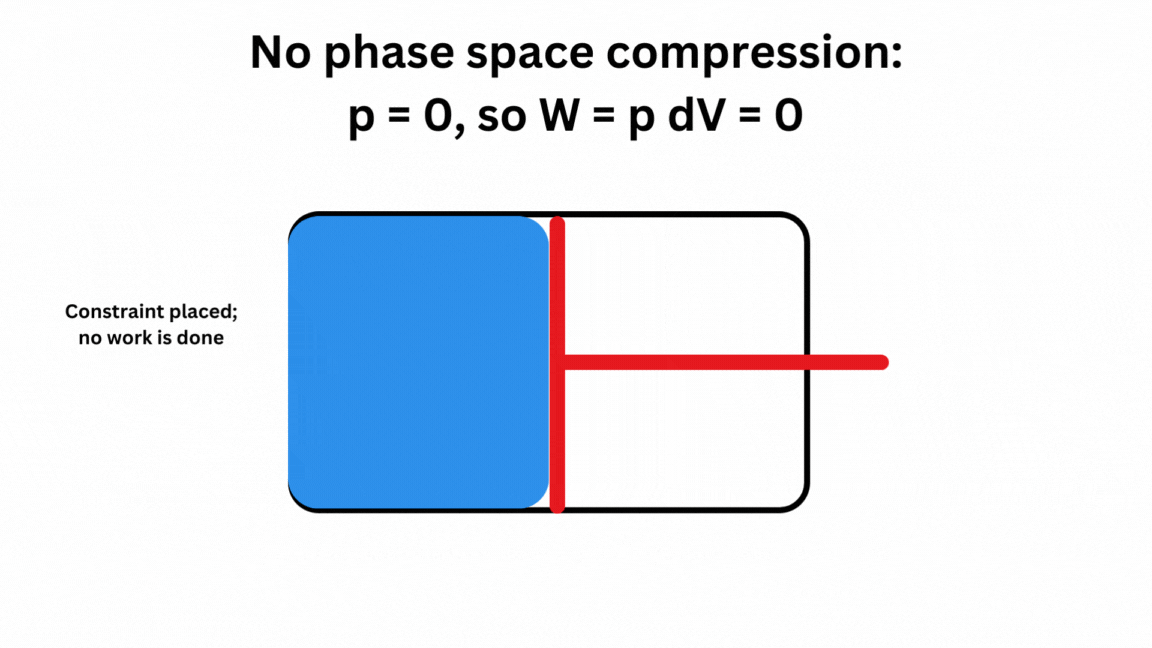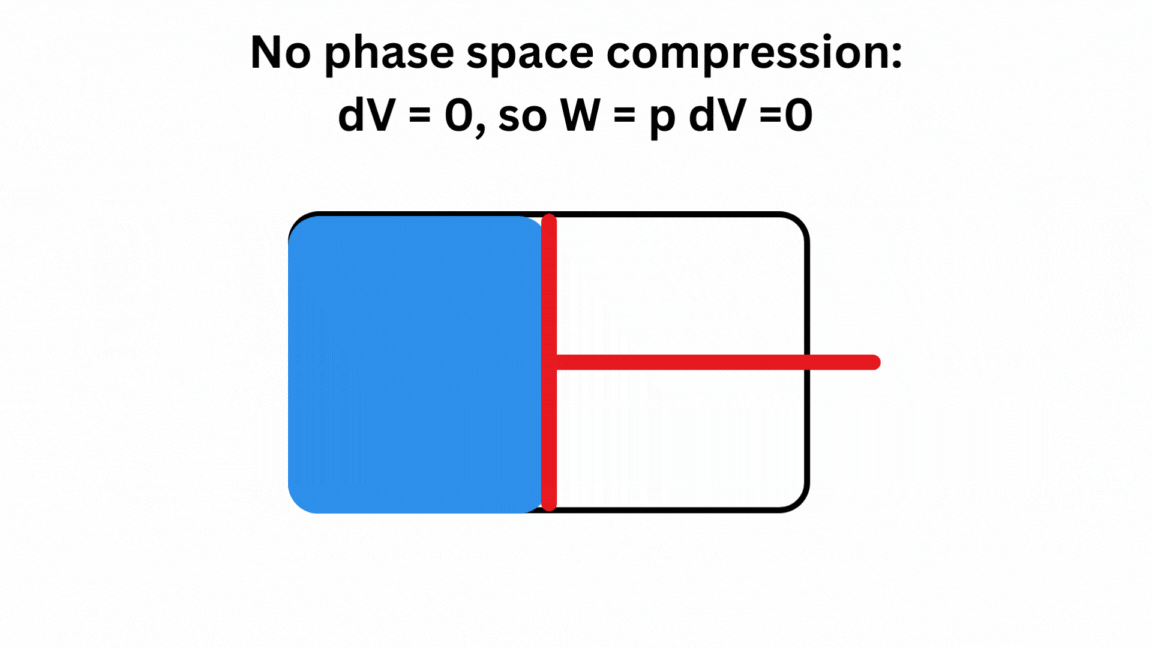
Here is a very basic animation of the proof that there is no real phase space compression in the “merging of two computational paths” if these involve a determinate fact of the matter about a system’s state. The example is a gas molecule, serving as a memory storage device, that could be either on the left or the right side of a box of volume V. Case 1 shows the case for true phase compression, while Case 2 shows a reset of classical information involving ignorance of the system’s actual state. In Case 2, there is ‘erasure’ of classical information, but there is no real phase space compression–i.e., no free energy expended since zero thermodynamic work is done in the reset, contrary to the traditional assumption. Thus, Landauer’s Principle in its traditional form fails. there is only an entropy costs of k ln 2 for case 1.
For those who want a concise proof that Landauer’s Principle does not apply to Case 2, here it is for an isothermal reset:
W(V_inital to V_final ) = NkT ln [ (V_final)/(V_initial)]
= NkT ln [ (V/2)/(V/2)]= NkT ln 1 = 0.